এবারে কোনো বর্তনীতে একাধিক রোধ থাকলে সেগুলোকে কীভাবে একটি ভুল্য রোধ হিসেবে বিবেচনা করা যায় আমরা সেই বিষয়টি দেখে নেই । 11.03 চিত্রের সার্কিটে দুটো রোধ লাগানো আছে, যেহেতু C ভূমিসংলগ্ন তাই তার বিভব শূন্য এবং A এর বিভব V। আমরা B এর বিভব কত জানি না, কিন্তু এটুকু জানি যে এবং দুটোর ভেতর দিয়েই সমান পরিমাণ বিদ্যুৎ I প্রবাহিত হচ্ছে। আমরা এমনিতেই বলে দিতে পারি যে দুটো রোধের যোগফলটি হবে মোট রোধ R এবং বিদ্যুৎ প্রবাহ হবে 1 = V/R কিন্তু সেভাবে না লিখে আমরা বরং এটা প্রমাণ করে ফেলি।
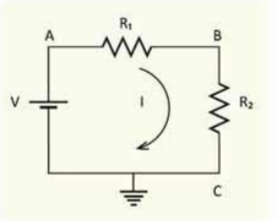
চিত্র 11.11: একটি বর্তনী বা সার্কিটে দুটি রোধ পরপর লাগানো।
যদি ধরে নিই B এর বিভব তাহলে প্রথম রোধএর জন্য লিখতে পারি:
আবার দ্বিতীয় রোধ এর জন্য লিখতে পারি :
কাজেই
কাজেই
আমরা এবং এই দুটি রোধকে একটি রোধ হিসেবে কল্পনা করতে পারিঃ
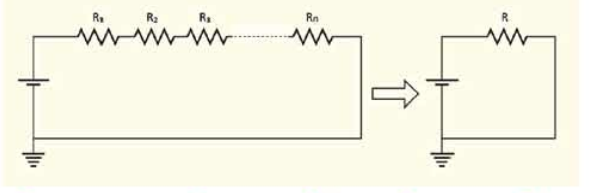
চিত্র 11.12: অনেক গুলো পর্যায়ক্রম রোধকে একটি তুল্য রোধ হিসেবে কল্পনা করা যায়।
যদি এখানে দুটি না হয়ে তিন-চারটি বা আরো বেশি রোধ থাকত (চিত্র 11.12) তাহলেও আমরা দেখাতে পারতাম যে সেগুলোকে সম্মিলিতভাবে একটি রোধ R কল্পনা করতে পারি বেটি সবগুলো রোধের যোগফলের সমান। এটাকে তুল্য রোধ বলে। অর্থাৎ যখন কোনো সার্কিটে রকম অনেকগুলো রোধ পরপর থাকে (শ্রেণি বর্তনী} তখন তাদের তুল্য রোধ
আরও দেখুন...